之前有一个同事问我,如何对一个非常大的数组进行排序,最开始的思路是:化整为零 合并排序。但实际上具体的一些细节还是有待商榷,因此 这里写一篇文章来具体来总结一下。
问题
假如一个数组中有1亿个数字,那么要对这个数组从小到大进行排序,我们该如何操作!
思路
其实对于这种数据量比较大的问题,思路基本上都是一致的:
- 首先,化整为零,对于那么大的一个数据,我们肯定不能直接对其进行操作,而是采用
某种方式将这个数组划分成多个比较小的数组; - 然后,我们在对这些比较小的数组采用
某种方式进行排序; - 最后,我们将所有排好序的数组采用
某种方式合并到一个数组中。
实现
从上面的思路可以看出 要完成对这个大数组的排序,我们需要三个步骤,这三个步骤中我们可以采用不同的方法。下面我们就详细的看一下 每一步我们可以采用什么方法。
化整为零
那么我们采用何种方法化整为零呢?其实要看我们后面的算法需求(数组合并),化整为零其实就是将这个很大的数组分成若干个小块。
那么这些小块之间有什么关系呢? 有序还是无序?
数组间是有序的
如果我们要求划分出的数组块之间是有序的 也就是说 第一个数组块中的数 均小于第二个数组块中的数,那么我们很容易想到 快速排序 根据一个中间值 一次排序就可以将整个数组分成两部分,左边的比中间值小右边的比中间值大。
快速排序,思路其实是递归。但是这一步其实我们只是想将这个数组分组。那么我们可以设置一个表示每个子数组块大小的值。在递归的过程中 如果发现子数组的长度已经小于等于这个值 那么我们第一步化整为零完成。退出这次的快速排序。
注意: 对于子数组的大小,个人感觉不需要过小(<1000),因为如果采用快速排序进行分组,如果要分成每组只有1000条数据,递归的层数约为15层 个人感觉这属于比较深的递归了。需要考虑是否会造成内存溢出。
内存溢出:
溢出的意思就是越界,操作系统会给每个进程分配一个最大上限的堆栈空间,如果超过了这个内存空间大小程序就会coredump,就像你使用int *pi = new int[100000000];会崩溃一样,因为这里堆溢出了。
操作系统分配给一个进程的栈空间是2M,堆空间在32位机器上是4G。如果你的进程的栈空间使用超过了2M就会栈溢出,堆使用超过4G就会堆溢出。
那么递归为什么会导致栈溢出呢?相信大家知道栈的出入规则,先入后出,递归的话那么先入的一直不能出栈,会一致存在栈空间中,这样就容易导致栈满而溢出。
若递归调用次数太多,就会只入栈不出栈,于是堆栈就被压爆了,此为栈溢出
数组间是无序的
如果我们对划分出来的子数组间没有要求,那么我们可以很简单的 通过一个表示子数组长度的值,将这个大的数组划分成多个小的数组。
不过如果不要求子数组之间是否有序,那么我们可以让数组的大小尽可能小(空间换时间),方便后面对子数组进行排序。
对较小的数组排序
对一个相对较小的数组排序的方法有很多,快速排序 选择排序都可以考虑。
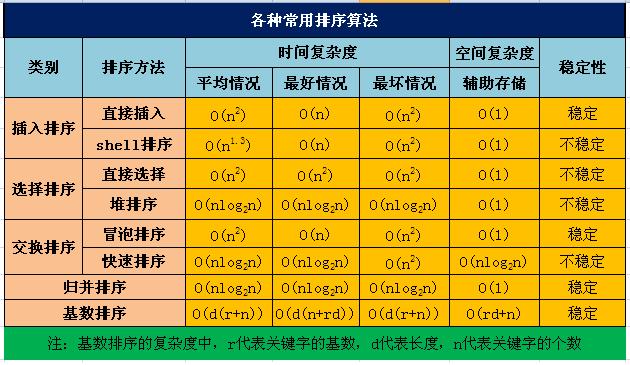
这里贴一张图,常用的算法的时间和空间复杂度:
数组合并
数组的合并,如果在第一步的时候选择的是划分子数组之间是有序的,这一步我们只需要将划分好的数组合并一下就可以了。这样就可以实现对这个大的数组的排序。
如果第一步我们选择的是子数组间无序,那么我们就要在合并的时候,我们可以采取类似归并排序的方法对这些长度较小的数组进行合并。
总结
上面所说的方法其实都可以实现排序的功能。但是对于数据非常多的情况,通常我们将数据全部读入内存在进行排序是非常困难的,因此在第一步的时候,如果我们选择的是将整个数据划分成有序块.那么我们要把所有的数据读到内存,而且快速排序的使用递归的思路更是大大的加大了排序过程中的内存占用。因此,一般情况 我们都采用先划分成小块(无序),然后每一个小块排序完成之后在进行多路归并排序。