几种常用的排序算法

这里总结了一下我们平时常用的集中排序方法，供大家学习参考

1、插入排序

每次从无序表中取出第一个元素，把它插入到有序表的合适位置，使有序表仍然有序。

直接插入排序算法时间复杂度：O(n^2)；空间复杂度：O(1)。直接插入排序是稳定的排序方法。

#include<iostream>
using namespace std;
int main()
{
    int a[]={98,76,109,34,67,190,80,12,14,89,1};
    int k=sizeof(a)/sizeof(a[0]);
    int j;
    for(int i=1;i<k;i++)//循环从第2个元素开始
    {
        if(a[i]<a[i-1])
        {
            int temp=a[i];
            for(j=i-1;j>=0 && a[j]>temp;j--)
            {
                a[j+1]=a[j];
            }
            a[j+1]=temp;//此处就是a[j+1]=temp;
        }
    }
    for(int f=0;f<k;f++)
    {
        cout<<a[f]<<"  ";
    }
    return 0;
}

2、冒泡排序

冒泡排序时间复杂度，最好情况：数组已有序O(n)；最坏情况:数组反序O(n^2)，平均时间复杂度：O(n^2)。空间复杂度，冒泡排序是原地排序，空间复杂度为O(1)。冒泡排序算法是稳定的排序算法。

void bubble_sort(int a[], int n)
{
    int i, j, temp;
    for (j = 0; j < n - 1; j++)
        for (i = 0; i < n - 1 - j; i++)
        {
            if(a[i] > a[i + 1])
            {
                temp = a[i];
                a[i] = a[i + 1];
                a[i + 1] = temp;
            }
        }
}

3、直接选择排序

无序数组a[0…n-1]，第一次从a[0]~~a[n-1]中选取最小值，与a[0]交换，第二次从a[1]~~a[n-1]中选取最小值，与a[1]交换，….，第i次从a[i-1]~~a[n-1]中选取最小值，与a[i-1]交换，…..，第n-1次从a[n-2]~~a[n-1]中选取最小值，与a[n-2]交换，总共通过n-1次，得到一个按关键字从小到大排列的有序序列·

在直接选择排序中，共需要进行n-1次选择和交换，每次选择需要进行 n-i 次比较 (1<=i<=n-1),而每次交换最多需要3次移动，因此，总的比较次数C=(n*n - n)/2，时间复杂度O(n^2)。直接选择排序为原地排序，空间复杂度O(1)。直接选择排序不是稳定的排序算法。

//直接选择排序  
void sort(int array[],int size){  
        int i,j,small,temp;  
        for(i=0;i<size;i++){  
        //将i假设为最小的  
                small = i;  
        //从i+1开始遍历，找到最小的但是比i大的数的下标  
                for(j=i+1;j<size;j++){  
                        if(array[j]<array[small]){  
                                small = j;  
                        }  
                }  
        //将i和找到的最小的数交换  
                temp = array[i];  
                array[i] = array[small];  
                array[small] = temp;  
  
                display(array,size);  
        }  
}

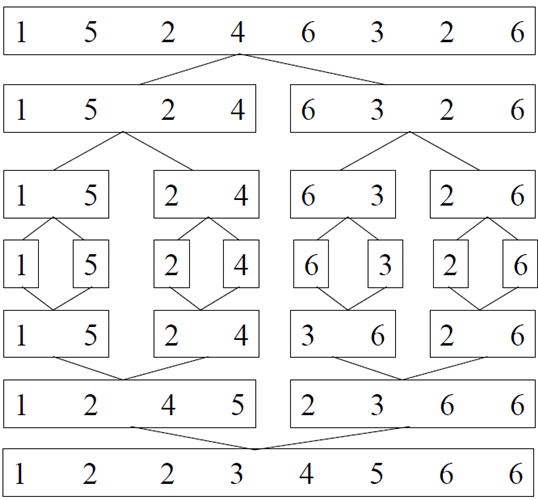
4、归并排序

时间复杂度为O(nlogn) 是归并排序算法中最好、最坏和平均的时间性能。空间复杂度O(n)。归并排序比较占用内存，但却是一种效率高且稳定的排序算法算法。

icon

void Merge(int sourceArr[],int tempArr[], int startIndex, int midIndex, int endIndex)
{
    int i = startIndex, j=midIndex+1, k = startIndex;
    while(i!=midIndex+1 && j!=endIndex+1)
    {
        if(sourceArr[i] > sourceArr[j])
            tempArr[k++] = sourceArr[j++];
        else
            tempArr[k++] = sourceArr[i++];
    }
    while(i != midIndex+1)
        tempArr[k++] = sourceArr[i++];
    while(j != endIndex+1)
        tempArr[k++] = sourceArr[j++];
    for(i=startIndex; i<=endIndex; i++)
        sourceArr[i] = tempArr[i];
}
 
//内部使用递归
void MergeSort(int sourceArr[], int tempArr[], int startIndex, int endIndex)
{
    int midIndex;
    if(startIndex < endIndex)
    {
        midIndex = (startIndex + endIndex) / 2;
        MergeSort(sourceArr, tempArr, startIndex, midIndex);
        MergeSort(sourceArr, tempArr, midIndex+1, endIndex);
        Merge(sourceArr, tempArr, startIndex, midIndex, endIndex);
    }
}

5、快速排序

快速排序算法平均时间复杂度O(nlgn)，最坏O(n^2)。快速排序需要栈空间来实现递归，如果数组按局等方式被分割时，则最大的递归深度为 log n，需要的栈空间为 O(log n)。最坏的情况下在递归的每一级上，数组分割成长度为0的左子数组和长度为 n - 1 的右数组。这种情况下，递归的深度就成为 n，需要的栈空间为 O(n)。快速排序不是稳定排序算法。

算法说明：
icon

void sort(int *a, int left, int right)
{
    if(left >= right)/*如果左边索引大于或者等于右边的索引就代表已经整理完成一个组了*/
    {
        return ;
    }
    int i = left;
    int j = right;
    int key = a[left];
     
    while(i < j)                               /*控制在当组内寻找一遍*/
    {
        while(i < j && key <= a[j])
        /*而寻找结束的条件就是，1，找到一个小于或者大于key的数（大于或小于取决于你想升
        序还是降序）2，没有符合条件1的，并且i与j的大小没有反转*/ 
        {
            j--;/*向前寻找*/
        }
         
        a[i] = a[j];
        /*找到一个这样的数后就把它赋给前面的被拿走的i的值（如果第一次循环且key是
        a[left]，那么就是给key）*/
         
        while(i < j && key >= a[i])
        /*这是i在当组内向前寻找，同上，不过注意与key的大小关系停止循环和上面相反，
        因为排序思想是把数往两边扔，所以左右两边的数大小与key的关系相反*/
        {
            i++;
        }
         
        a[j] = a[i];
    }
     
    a[i] = key;/*当在当组内找完一遍以后就把中间数key回归*/
    sort(a, left, i - 1);/*最后用同样的方式对分出来的左边的小组进行同上的做法*/
    sort(a, i + 1, right);/*用同样的方式对分出来的右边的小组进行同上的做法*/
                       /*当然最后可能会出现很多分左右，直到每一组的i = j 为止*/
}

更新于 2020-12-05

算法 # 排序冒泡快排